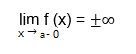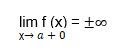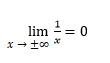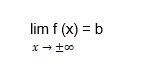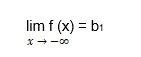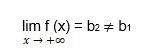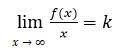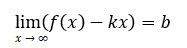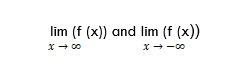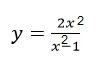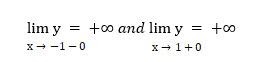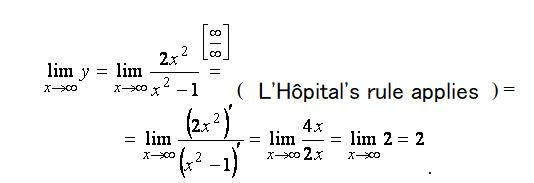Despite technological advancements, mathematics is employed everywhere in the current world. That is why academic institutions stress pupils studying this subject. High schoolers have the biggest challenges since they must construct graphs, determine the degree of the numerator or denominator, and do various other sophisticated activities. Today, we’ll focus on the horizontal asymptote rules, which students often ask questions.

What are horizontal asymptote rules?
In many circumstances, it is easier to create the function graph if you first plot the curve’s asymptotes. But, unfortunately, the asymptote’s path is full of tragedy. Consider what it would be like to spend your entire life moving in a straight line toward a treasured goal, getting as near as possible yet never reaching it. So is the case with the asymptote: it always attempts to reach a function’s curve graph, approaching it at the shortest possible range but never touching it.

According to the accepted definition, Asymptotes are infinitely long straight lines that near but do not meet the function you generated. As a result, the variable tends to have positive infinity or minus infinity at the exact moment. Vertical, oblique, and horizontal asymptotes are among the many types of asymptotes.

Vertical Asymptote
If the point x = a is a breakpoint of the second type, the vertical line x = a is the vertical asymptote of the graph of a function. For example, the vertical asymptote of the graph of the function f (x) is defined as the straight line x = a if at least one of the following requirements is met:

• The function’s limit is equivalent to plus or minus infinite when the argument’s value tends to some value “a” on the far left.

• The limit of the function is equivalent to plus or minus infinity when the value of the input tends to a certain value of “a” from the right.

Look for the vertical asymptotes of the function’s graph at the points of discontinuity and the domain of definition’s boundaries. There are no vertical asymptotes on the graph of a continuous function on the entire number line.

Oblique Asymptote
The above-mentioned vertical asymptote is always parallel to the cartesian coordinates. As a result, we only need a single integer to create a location on the x-axis or ordinates through which the asymptote crosses. More is needed for the slant asymptote—the angular following coefficient k, representing the line’s gradient. The x-intercept indicates how much above or below the origin of the line is.

As a result, the graph of a function cannot have more than two oblique asymptotes in any fashion. Otherwise, your calculations were erroneous. It is common to practise to group infinities under a single record when the graph approaches a single oblique asymptote. It would be helpful if you had the following oblique asymptote equation:

Horizontal Asymptote
According to the horizontal asymptote rules, the horizontal asymptotes are parallel to the Ox axis, which is the first thing to know about them. If we had a function that worked like this:

The horizontal line of the curve line y = f(x) is then y = b. At k = 0, the horizontal asymptote is a particular case of an oblique one. We’ll go over horizontal asymptote rules in greater depth because they’re so common in geometry assignments.

Asymptote Rules
The following rules apply to finding the horizontal asymptote rules of a function’s graph:

• Theorem 1

Allow the function y = x to be defined at minimum in some quasi-neighbourhood of the point x = a, with at least one of its one-sided limits equivalent to + or -. The vertical asymptote of the graph function is, therefore, a straight line. As a result, the vertical asymptotes of the function’s graph must be found at the function’s discontinuity points. Or the boundaries of its definitional realm.

• Theorem 2

Assume that the function y = f (x) is constructed for argument values that are high enough in absolute value and that the function has a finite limit. The horizontal asymptote of the graph function y = f(x) is a straight line y = b. It’s possible that:

And

B1 and b2 are finite values in the specified functions, and the graph features two separate horizontal asymptotes: left and right-sided. The graph has one left-sided or right-sided horizontal asymptote if only one of the finite limits, b1 or b2, exists.

• Theorem 3

Assume that the function y = f (x) is defined for absolute values of the argument that are large enough and that there exist finite limits:

And

The straight line is thus the oblique asymptote of the function’s graph. There is no oblique asymptote if a minimum one of the mentioned boundaries is infinite. Like the horizontal asymptote, the oblique asymptote can only be one-sided.

What Are Horizontal Asymptotes and How Do You Find Them?
The horizontal asymptote of a function f (x) is a straight parallel line to the x-axis that the function f (x) approaches as it approaches infinity, as we mentioned before. The horizontal asymptote formula can thus be written as follows: y = y0, where y0 is a fixed number of finite values.

You must first identify y0 to get the horizontal asymptote of the function f (x). Calculating the limits will give you the value of y0:

The horizontal asymptote of the function f(x) is y = y0 if the result of at least one limit equals a finite number y0.

Horizontal asymptote rules and examples:
Finding horizontal asymptote y and x values involves a variety of geometric assignments. We’ll look at one of these problems and demonstrate how to solve it.

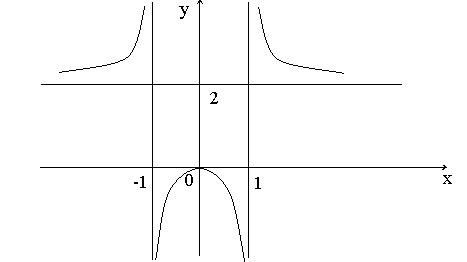
Find all of the asymptotes of the function’s graph:

Decision: At x (-∞, -1), U (1, +∞), the function is defined. Let’s look for its one-sided limits for x equals plus and minus 1.

The following calculations are based on the assignment:

We can no longer locate two other one-sided limits, as evident. The vertical asymptotes of the function’s graph are the straight lines x = -1 and x = 1. Let’s check the calculations:

As a result, the horizontal asymptote is the straight line. Therefore, we no longer need to hunt for oblique asymptotes now that the horizontal asymptote exists.

Solution: There are two vertical asymptotes x = ±1 and one horizontal asymptote y = 2 in the graph.

Glossary terms needed to find a horizontal asymptote
To better comprehend how to handle problems involving the computation of horizontal asymptote and to grasp the horizontal asymptote rules, you must first study the definitions of the following terms:

• The numerator is the number above the fractional bar. The numerator indicates how many portions of the total were taken.
• The denominator is the number below the fractional bar. The denominator indicates how many equal pieces are split from the whole.
• A rational function is obtained by performing a finite amount of arithmetic operations on the variable x and an arbitrary polynomial.
• Multiple multiplications are the definition of exponential growth. The more value the function receives, the faster it expands.
• To better understand horizontal asymptote rules, you need to understand the basics of a function’s graph. A function’s graph is a collection of points (x; y), where x is the parameter and y is the function’s value matching the supplied input.

Frequently Asked Questions

What is an asymptote?

Asymptotes are endless linear lines that approach the function you generated as closely as possible without touching it.

What are the different types of asymptotes?

Vertical, horizontal, and oblique asymptotes are the three types of asymptotes.

How can horizontal asymptotes be found?

The degrees of the numerator and denominator of a rational function can calculate the horizontal asymptote.

What do we need to follow horizontal asymptote rules?

Horizontal asymptote rules help describe the behaviour of a graph as the input becomes extremely big or very tiny. In contrast, vertical asymptotes help describe the behaviour of a graph as the output becomes very large or very small.

Total Assignment Help
Incase, you are looking for an opportunity to work from home and earn big money. TotalAssignmenthelp Affiliate program is the best choice for you. 

Do visit :https://www.totalassignmenthelp.com/affiliate-program for more details

Total Assignment help is an assignment help Online service available in 9 countries. Our local operations span across Australia, US, UK, South east Asia and the Middle East. With extensive experience in academic writing, Total assignment help has a strong track record delivering quality writing at a nominal price that meet the unique needs of students in our local markets.

We have specialized network of highly trained writers, who can provide best possible assignment help solution for all your needs.  Next time you are looking for assignment help, make sure to give us a try.