Importance and Progression Of The Quadratic Equation Solver

Question

Task: Provide a brief note on the evolution of quadratic equation.

Answer

Background
The discipline of mathematics is very complex and highly dependent on each of its subcategories which have been evolved into the present form by carrying out a lot of researches through whole centuries. The new theories and ideologies have helped in solving a lot of crucial problems in the scientific and real-life world. To make the discipline more attractive and accessible for the normal person with below-par intellect a major series of research has been conducted for the simplification of tough concepts. The advent of quadratic equations had overly simplified the calculations in the discipline of mathematics and thus have the new students in adopting the attracted new students for pursuing their academic career in the discipline of mathematics.

The term mathematics was derived from the word mathemata , that was used in the Greek language to denote a certain set of study or subject. Since the earlier period of history, mathematics had its scope widespread in all the branches of science and the daily life of a layman person. By the study of the evolution of any theory in the branch of mathematics, you could trace down the chronological and systematic study of the science. In the development of science, the researchers have faced a lot of problems and restrictions and it was the branch of mathematics that had solved the intriguing problems. By studying the evolution of mathematics, the student could also find inspiration in deriving new theories and solving challenging questions. Below are given some of the evident scopes of teaching the mathematic history in the classrooms.

• Increases the ability to learn the difficult aspects of mathematics.
• Displays the significance of mathematics in portraying the cultural human endeavor.
• The teachers could take a more authentic and pedagogic approach since they would be thorough about the reason and history of theories in the discipline.
• The actual nature and reason behind every approach could be justified.
• The prejudice that mathematics is a very hard subject to study could be eliminated.

In this report, our major aim is to study the evolution and scope of the quadratic equation solver.

The plot of quadratic equation solver evolution
If traced down to the evolution of the quadratic equation solver, it could be observed that the existence of the method in the world is almost older than 4000 years. The Babylonian tablets relevant to the theorem of the quadratic equation solver dates back to 1600 BCE. In the tablet, the diagonals pertaining to the square are predicted with the accuracy level of five decimals. The methodology we see today regarding the quadratic equation solver has been evolved in recent years. This was made possible only after the branch of algebra had been matured in the late 15th century.

The provided Babylonian tablet in this report is a piece of very crucial evidence and source on the principle for dealing with the various sets of number bases. It should be taken into account that the mathematician of Babylonia used the bases for calculations as 10 and 60. The Clay tablet also throws light on the area of decimal approximation and the estimation of irrational numbers and finding roots by a quadratic equation.

The depicted tablet provides the calculation in the below form,

The tablet could be displayed numerically as below.

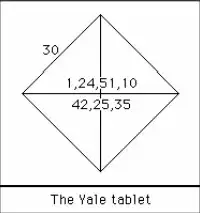
By looking at the tablet, you may wonder how they have developed this technology. The mathematicians of Babylonia had taken the geometrical approach in calculating the quadratic equations. Although the approach was geometrical, the end result was algorithmic in character.

Let us take a rectangle with area 2 sq. unit. By reducing the surplus area alongside the length of the rectangle, you could generate a square from it (Note that the new length should be equal to the breadth of the selected rectangle).

What actually is the quadratic equation solver?
It is the easiest and efficient method to find the root of the quadratic equations. The basic equation used in the quadratic equation solver is of second degree which could be represented by ax² + bx + c = 0, provide the condition that a could not be equal to zero. The numerical value of the variable x in the quadratic equation is termed to be the root of the equation. In other words, the value of x that provides the equation with equality to the value provided at the right-hand side is called root. Depending on the coefficients of the variable, the number of roots for the equation would root from 0 to 2. There are no limitations on the coefficients of the variable and hence they could real or imaginary numbers, real or complex.

If you are a student of the mathematic discipline, then you would have clarity that by using the generic quadratic equation solver, you could solve or find the root of the problem provided in the quadratic equation. Unlike other approaches, the quadratic equation solver is a much easier and error-proof tool for solving quadratic equations. This approach would also help in understanding the algorithmic operations.

The subdiscipline of algebra had been developed to solve various problematic equations. The approach of algebra could help in analyzing and estimating multiple unknown variables. The problems may require multiple values from multiple equations by the means of conducting a series of algebraic operations.

As mentioned in this article earlier, the simplified theory for quadratic equations had been developed in Babylonia around 4000 years ago. The necessity to find the square root of the land area or to allot the work to the employees had led the way for the development of this approach. Not limiting to this, the scope of quadratic equations also reached the area of astronomy. It has been observed from the ancient scripts and cuneiform writing that it consisted of a well developed and partial quadratic equation.

Scope of Quadratic equation solver
If you have to conduct a high end and advanced study of mathematics, it is very crucial that you should have a very good grasp on the quadratic equations. The scope of quadratic equations is not only limited to the discipline of mathematics, it also has a great significance in the branches of physics and chemistry. The teachers and tutors often have observed most of the students of mathematics find it very hard to do arithmetical operations on equations, especially the second-degree equations. Most of the students find it very hard to follow the conceptual or relational aspect of the quadratic equation and hence focus only on the procedural and instrumental factors. A better understanding of the quadratic equation is very significant for pursuing his higher degrees in the discipline of mathematics, which if ignored would cause a great barrier to his forward course in his academic career.

Different mathematicians in a different part of the world have different explanations and theorems on the topic of quadratic equations. Famous mathematician Sonnerhead had observed in his studies that the countries like Sweden had neglected some of the important concepts regarding the quadratic equation in their program of mathematic studies. This move has actually made the students aloof from the concepts of mathematics and they are finding it very hard to understand the theories which even remotely deals with the quadratic equation. As per the survey conducted by Lima and Tall in the year of 2010, it was observed that the students of the institutes where the concepts of quadratic equations were taught have displayed great reasoning abilities and sharpness in solving mathematical problems. The students have also displayed great progress in solving the problems containing advanced algebraic operations. The student should be well acquainted with different types and variants of the quadratic equation solver rather than providing them with a conventional format. Apart from learning the conventional format of ax² + bx + c = 0, the students should also be provided with the factored format, a (x – r₁) (x – r₂) = 0 and the vertex form, a (x – h)² + k = 0