Corporate Financial Management Assignment: Questions and Answers

Question

Task: 1 - 6 carry equal marks of 13 each, question 7 carries 22 marks. Answer all questions
Q1. Answer the following questions.
a. What is the Optimal Capital Structure Explain with a graph.
b. What is diversification in Finance Explain.
c. Explain the differences between American and European options.

Q2. Provide appropriate answers to the following questions.
a. What are differences between future and forward contracts Explain.
b. Explain 3 forms of market efficiencies.
c. Explain the term structure of interest rates.

Q3. If government bonds are currently paying 7 per cent and the inflation rate is 2.1 per cent, what is the approximate real rate What is the exact real rate
Q4. The following information relates to Rio Tinto Mining Corporation. What is Rio Tinto’s weighted average cost of capital
10 years ago, Rio Tinto issued 80,000 bonds with 16 years maturity and a face value of $1000 each, pays an – annual coupon amount of $100 each. The yield on the bonds is 15% p.a. Rio Tinto’s marginal corporate tax rate is 30%.
Rio Tinto has 15 million preference shares on issue, which are currently trading for $3.20 each, giving total market value of $48 million. They pay an annual dividend of 30 cents per share.
Rio Tinto has 21.5 million ordinary shares on issue, which are currently trading for $4 each. These shares are expected to pay an annual dividend of $0.75 next year, and this dividend is expected to grow at the constant rate of 3% in perpetuity.

Q5. Use the following option quotes to answer the questions below.
Q6. You would like to invest in two shares A and B. The return on these shares over the next year depends on the state of economy, which will be described as “Boom”, “Normal”, “Slow” and “Recession”. The table below shows the probability of each of these states of economy, and the expected return on each share given each possible state of the economy. The correlation coefficient between shares A and B is 0.5.

a. What is the expected return on A and B shares
b. What is the standard deviation of A and B shares
c. What is the expected return on portfolio comprised of 55% invested in share A and the balance in share B
d. What is the standard deviation on portfolio comprised of 55% invested in share A and 45% invested in share B
Q7. The risky portfolio Q consists of 2,500 shares of Google and 7,500 shares of Yahoo. Assume that Google has a share price of $4, an expected return of 18 per cent, and a standard deviation of 25 per cent. Yahoo has a share price of $2, an expected return of 15 per cent, and a standard deviation of 20 per cent. The correlation between the two is 0.5, and the risk-free rate of interest is 2 per cent.
What fraction of your portfolio must you invest in risky portfolio of Q and risk-free to have a portfolio standard deviation of 12 per cent

Answer

c. What is the Optimal Capital Structure Explain with a graph.
Solution
The capital structure can be characterized as the proportion of capital products in an entity's balance sheet. The capital structure of a company with a mixture of different capital instruments prevails in the industry, such as preference shares, bonds, shares, etc.

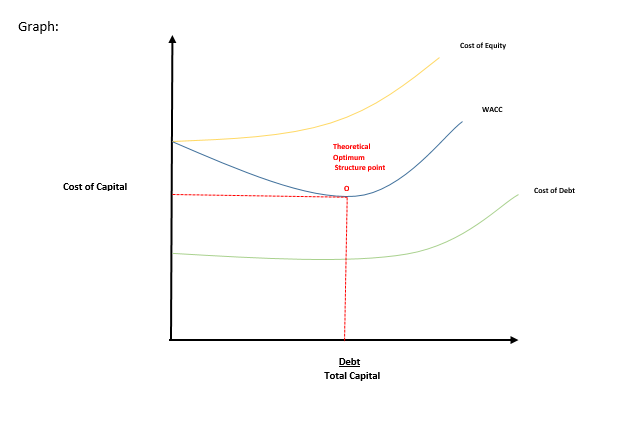
A growing portion of capital also has a cost factor attached to it. And different capital instruments have different costs.

So ideal capital structure can be said to be an ideal combination or the weighting should be optimal so that the cost part remains low, i.e. WACC stays small and the importance of the company will be maximized.

Through this table, we will examine how various financial instruments influence the expense of the resources of the enterprise. Debt is generally less costly because tax incentives are added to it and the cost of equity is significantly more expensive.
WACC lies between these two, as it takes advantage of all instruments and operates optimally so that costs remain small and profits remain higher.

d. What is diversification in Finance Explain.
Solution
Diversification in finance means acquiring resources in a portfolio of financial securities, including stock, bonds, futures, etc. Diversification helps to compensate for the loss of one asset from the gain of the other asset. Any commodity in which the money is invested does not respond in the same way and produces different results that can be either negative or positive cash flow. Investors can identify different investments before making investments in each portfolio after weighing their risks, returns, holding times, etc. It is very important to invest funds in managed funds so that the money invested to give the investor a net benefit and not a net loss. Investors need to determine how much capital will be spent in shares, how much in stocks, how much in options, and so on, based on the number of financial instruments used in the portfolio.

c. Explain the differences between American and European options.
Solution
American Options:
The American Alternative consists of two types of approaches, Call Choice and Put Option. The investor has the right to exercise such an option before the date of the excise duty or the expiry date specified in the option plan. These options have their values attached to the underlying assets of these options. The bulk of American stocks are exchanged in much of the stock markets across the world. These options give an investor a more dynamic position so that he/she can exercise his / her right at any time, based on his / her experience and knowledge, and he/she is free to take this decision. These options are also riskier.

European Options:
In European Options, these options have an expiry date, but these options have little opportunity for buyers to exercise their right until the expiry date. As a result, the risk of buying European options has been high. Thanks to non-flexibility, the risk factor is very small and the margin is fairly poor compared to American alternatives. These Options begin to avoid trading in an exchange a day before the expiration date or the expiration day.

Q2. Provide appropriate answers to the following questions.
d. What are the differences between future and forward contracts Explain. Solution
• Forward contracts are flexible according to the conditions of the parties to such contracts, while futures contracts are fixed and not flexible. • Forward contracts are much more volatile than future contracts as there is no legal body to manage forward contracts and if any side refuses to perform its portion of the bargain, the other party to the contract will incur damage. • Forward contracts are settled on the maturity agreed date between the parties, while futures contracts are settled regularly. • Initial investment is not required when forward contracts are transacted compared to the future contract transactions where margin money is required.

e. Explain 3 forms of market efficiencies.
Solution
Weak Form: In this form of market form, the market is forecast based on historical prices. Historical trading information is generally used as a means of market analysis. In this method, trading technology and rules attempt to exploit historical data. These models are primarily popular in developed markets. As a consequence, this study does not have long-term results for the future. And, even in the short term, it's good.

Semi- Strong Form: This form implies that the use of fundamental analysis and technical analysis is not such a strong basis for giving the investor the advantage of instantly priced securities. At the end of the day, however, the public knowledge available at large is not that helpful to the production of full income. As a consequence, private knowledge that is largely inaccessible on the market or held in the possession of a small number of individuals can be beneficial in making full profits. Thus, an investor can not make more profits simply from public information because the market reacts quickly to information.

Strong Form: This type of market relies on both public and private information (data). But the use of confidential information is not constitutionally allowed in most countries because it leads to insider dealing. This form thus conveys that the market price consists of both private and public knowledge, and is a mixture of weak form and semi-strong form.

f. Explain the term structure of interest rates.
Solution
The word interest rate mechanism is a device that tells us the maturity of the investment security to the amount of interest it charges to the borrower. It is commonly referred to as the yield curve. The short-term debt interest rate fluctuates faster than long-term debt. Yet long-term debt rates are higher than short-term debt. The return curve is affected by the supply and demand of financial instruments . It depends on the strategy of the buyer and the seller of the loan. The buyer of the bond requires the bonds to mature then where it will take the capital, so that he prefers the bonds whose maturity date would be now where his capital need occurs. On the other hand, the seller needs the maturity period to be at the point when he would have received profit from some other source. The yield curve is also driven by the economic situation and the globe, by the measures implemented by the government to invest in bonds, and by tax rate changes.

Q3. If government bonds are currently paying 7 percent and the inflation rate is 2.1 percent, what is the approximate real rate What is the exact real rate
Solution
RR = ((1+Nr)/ (1+Inf))-1
RR = ((1+0.07)/ (1+0.021))-1
RR = (1.07)/ (1.021) – 1
RR = 4.799%
Where RR = Real Return
Nr = Interest rate of Govt. bond
Inf = Inflation Rate

Q4. The following information relates to Rio Tinto Mining Corporation. What is Rio Tinto’s weighted average cost of capital
10 years ago, Rio Tinto issued 80,000 bonds with 16 years maturity and a face value of $1000 each, pays an – annual coupon amount of $100 each. The yield on the bonds is 15% p.a. Rio Tinto’s marginal corporate tax rate is 30%.
Rio Tinto has 15 million preference shares on issue, which are currently trading for $3.20 each, giving a total market value of $48 million. They pay an annual dividend of 30 cents per share.
Rio Tinto has 21.5 million ordinary shares on issue, which are currently trading for $4 each. These shares are expected to pay an annual dividend of $0.75 next year, and this dividend is expected to grow at a constant rate of 3% in perpetuity.

Solution
Bonds 80,000
Maturity = 16 years
F.V = 1000$ each
Coupon amount $100 each
Coupon rate = 100/1000=10%
Yield Rate = 15% P.A
Tax rate = 30%
Years remaining for Maturity = 6 years (16-10)
The weighted average cost of capital (WACC)
WACC = (E/V) Re + (P/V) Rp + (D/V) Rd (1 – t)
D = Market value of Debt = (Number of Bonds issued x Value of Each Bond)
= 80,000 x 1000$ = 80,000,000 = $ 80 million
P = Market value of Preference Shares
= Number of Preference Shares issued x Price per preference share
= 15,000,000 x $3.20 = $48 million
E = Market Value of Equity
= Number of equity shares issued x Trading or Market value
= 21.5 million x $4 = $ 86 million
V = Total Market Value
Total Market Value = D+P+E
Total Market Value = $80m + $ 48m + $ 86m
Total Market Value = $214m
Return on Preference Shares (Rp)
Return on Preference Shares = D/Po
Return on Preference Shares = $0.30/$3.20
Return on Preference Shares = 0.09375
Return on Preference Shares = 9.375%
Return on Equity Shares (Re)
Return on Equity Shares = (D1/Po) + g
Return on Equity Shares = (0.75/4) + 0.03
Return on Equity Shares = 0.2175
Return on Equity Shares = 21.75%
Return on Debt fund (Rd)
NP = Coupon/YTM
= $100/0.15 = $666.67
Rd = I + (PV-NP)/n
(PV+NP)/2
Rd = 100 + (1000-666.67)/6 (in$)
(1000+666.67)/2
Rd = 100+55.56
833.33
Rd = 0.1860 or 18.60%
Put all these values in equation: WACC = (E/V) Re + (P/V) Rp + (D/V) Rd (1 – t)
= ($86m/$214m) x 0.2175 + ($48m/$214m) x 0.09375 + ($80m/$214m) x 0.1860 x (1-0.30)
= 0.0874 + 0.0210 + 0.048673
= 0.157073
= 15.7037%
So WACC = 15.70% (Approx.)

Q5. Use the following option quotes to answer the questions below.
December, 2019, Alibaba Ltd
Last sale price $16.00
Calls – Last Puts - Last
Strike Price Jun July Aug Jun July Aug
$16.00 36 cents 48 cents 72 cents 24 cent 27 cents 32 cents

d. Suppose you buy 150 July $16.00 call contracts. How much will you pay, ignoring commissions
Solution
Amount without commission = (150 x 10,000 x $0.48)
Amount without commission = $7,20,000

e. Suppose you buy 50 of August 2019 put contracts. What is your maximum net gain
On the expiration date, Alibaba is selling for $14.00 per share. What are your options worth
Solution
Maximum total gain = 50 x 10,000 x ($16 - $0.32)
Maximum net total gain = $78,40,000

f. In part (b), suppose you sold your 50 August put contracts. What is your net gain or loss if Alibaba is selling for $13.00
Solution
For $13
Net total Loss = ($16 - $13 - $0.32) x 50 x 10,000
Net total Loss = $13,40,000
Assumption: 1 lot of call or put contract consists of 10,000 shares

Q6. You would like to invest in two shares A and B. The return on these shares over the next year depends on the state of the economy, which will be described as “Boom”, “Normal”, “Slow” and “Recession”. The table below shows the probability of each of these states of economy and the expected return on each share given each possible state of the economy. The correlation coefficient between shares A and B is 0.5.

e. What is the expected return on A and B shares
Solution
RA = pr
RA = (0.20 x 0.25) + (0.40 x 0.16) + (0.25 x 0.10) + (0.15 x -0.06)
RA = 0.05 + 0.064 + 0.025 – 0.009
RA = 0.13
RA = 13 %
RB = pr
RB = (0.20 x 0.21) + (0.40 x 0.12) + (0.25 x 0.08) + (0.15 x 0.05)
RB = 0.042 + 0.048 + 0.02 + 0.0075>
RB = 0.1175
RB = 11.75%
Where RA = Return of A
RB = Return of B
pr = Summation of Probability multiplied by Return

f. What is the standard deviation of A and B shares
Solution
For Brevity
r = return of a share
RA = Expected return of A (Average Return)
RB = Expected return on B (Average Return)
VA = Variance of A
VB = Variance of B
SD = Standard Deviation
VA = P (r – RA) ^ 2
VA = 0.20(0.25-0.13) ^2 + 0.40(0.16-0.13) ^2 + 0.25(0.10-0.13) ^2 + 0.15(-0.06-0.13) ^2
VA = 0.00888
SDA = (0.00888) ^0.5
SDA = 0.094234
SDA = 9.42%
VB = 0.20(0.21-0.1175) ^2 + 0.40(0.12-0.1175) ^2 + 0.25(0.08-0.1175) ^2 + 0.15(0.05-0.1175) ^2
VB = 0.002749
SDB = (0.002749) ^0.5
SDB = 0.052429
SDB = 5.24%

g. What is the expected return on a portfolio comprised of 55% invested in share A and the balance in share B
Solution
WA = Weightage of A
WB = Weightage of B
Rp = Expected Return of portfolio
Rp = (WA x RA) + (WB x RB)
Rp = (0.55 x 0.13) + (0.45 x 0.1175)
RP = 0.0715 + 0.052875
RP = 0.124375
RP = 12.44%

h. What is the standard deviation on portfolio comprised of 55% invested in share A and 45% invested in share B
Solution
Variance of Portfolio (Vp) =
((WA) 2 x (SDA) 2) + ((WB) 2 x (SDB) 2) + 2WAWB x (Correlation A, B) x SDA, SDB
= ((0.55) 2 x (0.0942)2) + ((0.45) 2 x (0.0524)2) + 2 (0.55) (0.45) (0.5) (0.0942) (0.0524)
= (0.3025 x 0.008874) + (0.2025 x 0.002746) + 0.001222
= 0.002684 + 0.000556 + 0.001222
= 0.004462
Standard Deviation of Portfolio (SDP) = Root of 0.00462 = 0.066798 or 6.68%
SDP = Standard Deviation of Portfolio
SDA = Share A’s Standard Deviation
SDB = Share B’s Standard Deviation

Q7. The risky portfolio Q consists of 2,500 shares of Google and 7,500 shares of Yahoo. Assume that Google has a share price of $4, an expected return of 18 per cent, and a standard deviation of 25 per cent. Yahoo has a share price of $2, an expected return of 15 per cent, and a standard deviation of 20 per cent. The correlation between the two is 0.5, and the risk-free rate of interest is 2 per cent.
What fraction of your portfolio must you invest in risky portfolio of Q and risk-free to have a portfolio standard deviation of 12 per cent
Solution
For Brevity,
WG = In portfolio of Q Google’s shares Weightage
WY = In portfolio of Q Yahoo’s shares Weightage
WQ = Q’s Portfolio Weightage
WR = Risk-Free Investment’s Weightage
SDQ = Q’s Portfolio’s Standard Deviation
SDG = Google’s shares Standard Deviation
SDY = Yahoo’s shares Standard Deviation
SDR = Standard Deviation of Risk-Free Investment
Google = $4 x 2500 = $10,000
Yahoo = $2 x 7500 = $15,000
Total Value = $25,000
Weightage = 40:60 or 40%/60%
Standard Deviation of Portfolio Q
The variance of Portfolio (Vp) =
((WG) 2 x (SDG) 2) + ((WY) 2 x (SDY) 2) + 2WGWY x (Correlation G, Y) x SDG, SDY
((0.4)2 x (0.25)2) + ((0.6)2 x (0.20)2) + 2 (0.4) (0.6) x (0.5) x 0.25 x 0.20
0.01 + 0.0144 +0.012
0.0364 = Variance
(0.0364)0.5 = 0.190788 or 19.07% (S.D = (Variance) 0.5)
SDQ = 19.07%
The standard deviation of risk-free securities are always “0”
So Correlation of Portfolio Q and Risk-free security (R) will be zero.
To find the weightage, we will use the following formula:
SDp = (WQ x SDQ) + (WR x SDR)
SDp = (WQ x SDQ) + ((1-WQ) x SDR)
0.12 = (WQ x 0.1907) + ((1-WQ) x 0)
0.12 = (WQ x 0.1907) + 0
0.12/0.1907 = WQ
WQ = 0.6292 or 63% Approx.
WR = 37%
So the Appropriate fraction to be invested between Portfolio of Q and Risk-free Investment will be 63:37