Statistics Assignment: Critical Discussion On Structural Reliability Analysis

Question

Task:
Prepare a statistics assignment presenting a critical discussion on structural reliability analysis.

Answer

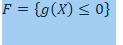
Monte Carlo Simulation Method
Monte Carlo Simulation Method provides a direct consideration on the various probability distribution for variables that are random and computation of the probability of failure during structural analysis (Zio, 2013). This methodology uses the capabilities of NN in approximation of functions that reproduces structural behaviors. In assessing the validity of the methodology we performed a test function on two structural examples as presented below. The results of the different set of random values and the probability functions are calculated over and over again.

Consider the equation below;

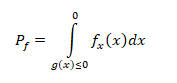
The analysis of the above equation can also be performed through simulations and this can be done through simulation techniques. The technique that we are going to consider here Monte Carlo Simulation technique.

From the above equation above we are going to provide the probability integral using the indicator function as shown below;

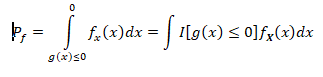
The function equation for the joint density above provides N outcomes for the simulation. This can be done in two basic steps;

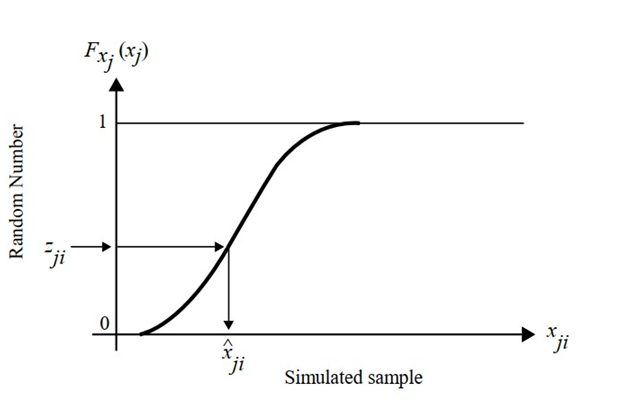
Monte Carlo Simulation have the following advantages compared;

• Probabilistic results show above are shown how it could happen but also how likely each outcome can occur.
• There is a provision for the model interdepended relationships between the input variables in Monte Carlo Simulations. The accuracy is represented and the reality in some factors may go and down accordingly and this is seen in the results.
• For Monte Carlo simulation its easy to perform and show both the sensitivity analysis and the deterministic analysis. This is because the inputs for the biggest effect on the bottom-line results are shown.
• Monte Carlo Simulation generates graphical results as shown above. The graphs of different outcomes can be generated and this also indicates occurrence chances. This makes it easier to communicate with the stakeholders about your findings.

First Order Reliability Methods (FORM).
The First-Order Reliability Method (FORM) approach is a perfect alternative to simulation for obtaining probabilistic estimates for reliability. Hasofer and Lind (1974) came up with an iterative formula that was used in the search of MPP (Most Probable Failure Point). This can be defined as a point on the failure surface that has a minimum distance from the origin available on the standard normal space. Thus for them they proposed that the main effort to FORM can be expressed using the following model.

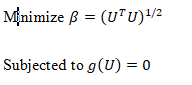
From the above formula we can derive the FORM Formula as shown in the below analysis.

The First Order Reliability Methods (FORM), is done through the Asymptotic Laplace Integral expansion (Niederreiter, 1998). We will start by defining the vector of random variables as follows;

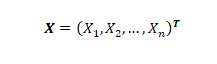
The above probability of failure can also be derived using the reliability index as follows;

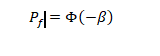
The above complements failure probability; and thus the reliability measure will be depicted in the form;

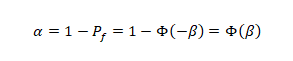
The above analysis can be expressed in the following diagram;

The advantage of FORM Over the other techniques is that for convergence purposes it only needs a small number of iterations (B. Keshtegar and M. Miri). This makes its computations to be efficient and accurate. In addition to that FORM has its random variables number increasing with a decrease in its efficiency.

Conclusion.

From the above analysis the MCS approach is more attractive compared to the FORM-Based approach. This is only when more variables and estimates are required. For precision and accuracy of the results then the other form is likely to be adopted in structural analysis.

Reference.
Melchers, R., & Beck, A. Structural reliability analysis and prediction.

Zio, E. (2013). The Monte Carlo simulation method for system reliability and risk analysis. Springer.

Nikolaidis, E., Ghiocel, D., &Singhal, S. (2005). Engineering design reliability handbook. CRC Press.

Niederreiter, H. (1998). Monte Carlo and Quasi-Monte Carlo methods 1996. Springer.

Cornell, C.A. (1969). A Probability Based Structural Code. ACI-Journal, Vol.66, pp.

974-985.

Basler, E. (1961) Untersuchungenüber den Sicherheitsbegriff von Bauwerken. SchweizerArchivfürangewandteWissenschaft und Technik

Hasofer, A.M. and Lind, N.C. (1974). An Exact and Invariant First Order Reliability Format. Journal of Engineering Mechanics. Div. Proc. ASCE.100(EMl), pp. 111-121.

Madsen, H.O., Krenk, S. and Lind, N.C. (1986). Methods of Structural Safety. Statistics assignment Prentice Hal, Inc. Englewood Cliffs, NJ 07632.

D. Yang, “Chaos control for numerical instability of first order reliability method,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. 10, pp. 3131–3141, 2010.

B. Keshtegar and M. Miri, “Introducing conjugate gradient optimization for modified HL-RF method,” Engineering Computations, vol. 31, no. 4, pp. 775–790, 2014.

A. MohammadiFarsani and B. Keshtegar, “Reliability analysis of corroded reinforced concrete beams using enhanced HL-RF method,” Civil Engineering Infrastructures Journal, vol. 48, no. 2, pp. 297–304, 2015.

B. Keshtegar and M. Miri, “An enhanced HL-RF Method for the computation of structural failure probability based on relaxed approach,” Civil Engineering Infrastructures Journal, vol. 1, no. 1, pp. 69–80, 2013.

B. Keshtegar and M. Miri, “Reliability analysis of corroded pipes using conjugate HL-RF algorithm based on average shear stress yield criterion,” Engineering Failure Analysis, vol. 46, pp. 104–117, 2014.

B. Keshtegar, “Chaotic conjugate stability transformation method for structural reliability analysis,” Computer Methods in Applied Mechanics and Engineering, vol. 310, pp. 866–885, 2016.