Statistics Assignment: Using Statistical Techniques to Solve Business Problems
Question
Task
The questions to be answered in this statistics assignment are;
Week 2 Question 1:
In your own words, differentiate the following statistical terminologies with some examples.
a. Population Parameter and Sample Statistic
b. Descriptive Statistics and Inferential Statistics
c. Nominal Scale and Ordinal Scale
d. Primary Data Source and Secondary Data Source
Week 3 Question 1:
Data showing the population by state in millions of people follow (The World Almanac, 2012).
a. Develop a frequency distribution, a percent frequency distribution, and a histogram. Use a class width of 2.5 million.
b. Does there appear to be any skewness in the distribution? Explain.
c. What observations can you make about the population of the 50 states?
Week 4 Question 2:
Forty-three percent of Americans use social media and other websites to voice their opinions about television programs (the Huffington Post, November 23, 2011). Below are the results of a survey of 1364 individuals who were asked if they use social media and other websites to voice their opinions about Television programs

a. Show a joint probability table.
b. What is the probability a respondent is female?
c. What is the conditional probability a respondent uses social media and other websites to voice opinions about television programs given the respondent is female?
d. Let F denote the event that the respondent is female and A denote the event that the respondent uses social media and other websites to voice opinions about television programs. Are events F and A independent?
Week 5 Question 3:
The average starting salary for this year's graduates at a large university (LU) is $20,000 with a standard deviation of $8,000. Furthermore, it is known that the starting salaries are normally distributed.
- What is the probability that a randomly selected LU graduate will have a starting salary of at least $30,400?
- What is the probability that a randomly selected LU graduate will have a salary of exactly $30,400?
- Individuals with starting salaries of less than $15600 receive a low income tax break. What percentage of the graduates will receive the tax break?
- If 189 of the recent graduates have salaries of at least $32240, how many students graduated this year from this university?
Week 6 Question 3:
The College Board reported the following mean scores for the three parts of the SAT (The World Almanac, 2009):
Critical reading 502
Mathematics 515
Writing 494
Assume that the population standard deviation on each part of the test is 100.
a) What is the probability that a random sample of 90 test takers will provide a sample mean test score within 10 points of the population mean of 502 on the Critical reading part of the test?
b) What is the probability that a random sample of 90 test takers will provide a sample mean test score within 10 points of the population mean of 515 on the Mathematics part of the test? Compare this probability to the value computed in part (a).
Answer
Statistics Assignment Week 2: Question 1:
a. Sample statistic is related with sample features and population parameter is related with population characteristics. The differences between the two statistical measures have been presented in the following table.
Table 1: Difference between Population Parameter and Sample Statistic
|
Descriptions |
Sample Statistic |
Population Parameter |
|
Computation |
It is computed from sample data. |
It is computed from the entire population. |
|
Measures |
Mean (), standard deviation (s), median etc. calculated from sample data. |
Mean (), standard deviation (), median etc. calculated/ prior knowledge considering the entire population. |
|
Characteristics |
Sample statistic is a random variable as it is calculated from random sampling (Siegel, 2016, p. 3-18). |
Parameter is a fixed number and generally unknown due to lack of data from entire population. |
|
Correspondence |
Sample statistic estimates the unknown population parameter. For example, sample mean is an unbiased estimator of the population mean. |
Population parameter is mostly unknown and estimated by sample statistic. The error is called error in estimation. For example, sample standard deviation cannot estimate population standard deviation in unbiased way. |
|
Example |
Sample mean evaluated from heights of students in a class. |
Population mean calculated from heights all the students in the University (seems unlikely!) |
b. Difference between Descriptive Statistics and Inferential Statistics is based on the fact that descriptive statistics present overall idea of the data, whereas inferential statistics help in drawing conclusive statements about the population based on probabilistic approach using parametric and non-parametric tests.
Table 2: Difference between Descriptive Statistics and Inferential Statistics
|
Descriptive Statistics |
Inferential Statistics |
|
|
Definition |
These kinds of statistics describe the population or sample under study. |
These type of statistics focuses on drawing conclusions about the population from sample data. |
|
Function |
Analyse, graphically organize data in reminiscent way(Lacort, 2014, p. 13-50). |
Compare and predict using different statistical tests (t-test, ANOVA, Chi-Square, Mann Whitney U test). |
|
Presentation |
Tables, graphs, statistical measures like mean, median, standard deviation etc. |
Probability of critical region and confidence interval. |
|
Objective |
Explain and summarize the data in a coherent manner. |
Draw conclusion about a population from sample data. |
|
Example |
Average score in mathematics is 78 with standard deviation of 12 in a class. |
At 95% confidence, try to assess/ compare with prior knowledge of the average marks of the entire school (population) using the information from the sample. |
c. Difference between Nominal Scale and Ordinal Scale is due to the difference in data types measured by the two scales.
Table 4: Difference between Primary Data Source and Secondary Data Source
|
Nominal Scale |
Ordinal Scale |
|
|
Definition |
Nominal scale variable does not have evaluative distinction. |
Ordinal scale variable has evaluative distinction. |
|
Measurement |
Levels of measurement are not comparable, and they do not have any lesser or greater relation. There can be qualitative difference (Wuensch, 2014, p. 70-120). |
Levels of measurement are comparable and have lesser or greater relation. There can be quantitative difference. |
|
Example |
Gender of participants can be coded as female = 0 and male = 1, are nominal scale measurements |
Preference in choice of products A = 1, B = 2, C= 3, D = 4 indicates that A is the most popular brand. |
|
Illustration |
Colour of eye balls Black =1, Brown = 2, Green = 3 are nominal scale measurements. |
Strength of vision as Strong = 1, Moderate= 2, and Weak = 3 implies quantitative grading. |
d. Difference between Primary Data Source and Secondary Data Source is primarily the root of the data collection. The difference is based on the fact that whether researchers personally collect data or sources it from any available resources such as website, book, journal, or newspaper.
Table 4: Difference between Primary Data Source and Secondary Data Source
|
Primary Data Source |
Secondary Data Source |
|
|
Origin |
Primary data source provides original and factual data. |
Secondary data source provides |
|
Collection Purpose |
Primary data is collected to solve problem available to the researcher. |
Secondary data source provides data to solve broader problem not at hand. |
|
References |
Primary data sources provide data for the first time (Hoelter et al., 2016, p. 651-661). |
Secondary data sources contain data in various platforms as a. website, book, journal, publications, or newspapers. |
|
Timeline |
Primary data sources provide real time data. |
Secondary data sources provide past data. |
|
Example |
Data collected by a researcher from employees regarding their body temperatures. |
Data collected from WHO website regarding COV-SARS2 deaths. |
Week 3: Question 2:
a. The frequency Distribution is in Table 5.
Table 5: Frequency Distribution of Population in 2012, USA
|
Class Limits |
Bins |
Frequency |
|---|---|---|
|
0.5-3 |
3 |
21 |
|
3.1-5.6 |
5.6 |
9 |
|
5.7-8.2 |
8.2 |
9 |
|
8.3-10.8 |
10.8 |
4 |
|
10.9-13.4 |
13.4 |
3 |
|
13.5-16 |
16 |
0 |
|
16.1-18.6 |
18.6 |
0 |
|
18.7-21.2 |
21.2 |
2 |
|
21.3-23.8 |
23.8 |
0 |
|
23.9-26.4 |
26.4 |
1 |
|
26.5-29 |
29 |
0 |
|
29.1-31.6 |
31.6 |
0 |
|
31.7-34.2 |
34.2 |
0 |
|
34.3-36.8 |
36.8 |
0 |
|
36.9-39.4 |
39.4 |
1 |
The percentage frequency Distribution is in Table 6.
Table 6: Percentage Frequency Distribution of Population in 2012, USA
|
Class Limits |
Bins |
Frequency |
Percentage Frequency |
|
0.5-3 |
3 |
21 |
42.0% |
|
3.1-5.6 |
5.6 |
9 |
18.0% |
|
5.7-8.2 |
8.2 |
9 |
18.0% |
|
8.3-10.8 |
10.8 |
4 |
8.0% |
|
10.9-13.4 |
13.4 |
3 |
6.0% |
|
13.5-16 |
16 |
0 |
0.0% |
|
16.1-18.6 |
18.6 |
0 |
0.0% |
|
18.7-21.2 |
21.2 |
2 |
4.0% |
|
21.3-23.8 |
23.8 |
0 |
0.0% |
|
23.9-26.4 |
26.4 |
1 |
2.0% |
|
26.5-29 |
29 |
0 |
0.0% |
|
29.1-31.6 |
31.6 |
0 |
0.0% |
|
31.7-34.2 |
34.2 |
0 |
0.0% |
|
34.3-36.8 |
36.8 |
0 |
0.0% |
|
36.9-39.4 |
39.4 |
1 |
2.0% |
Histogram for the above distribution is in Figure1.
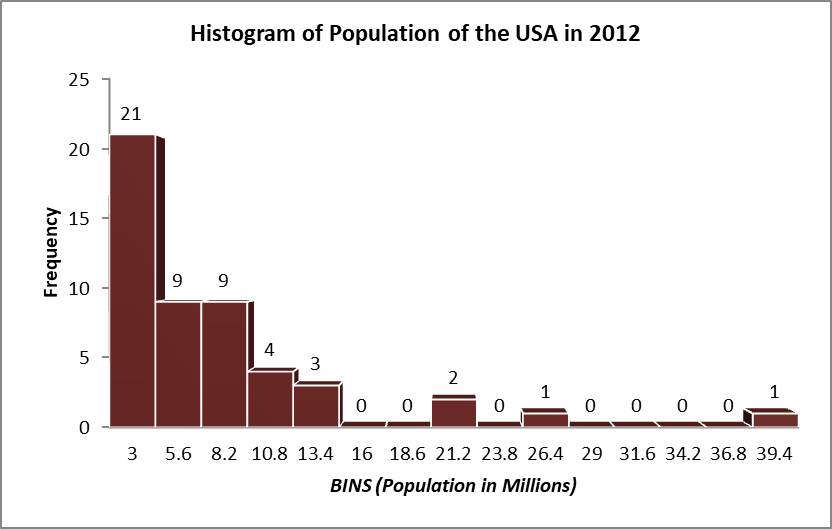
Figure 1: Histogram for Population for USA in 2012 (Source: State wise data)
b. From the histogram in Figure1 it can be seen that the distribution of population is highly right/ positively skewed. There were four states with outlier/ unusually higher population compared to other 46 states. Also, population in most of the states (21 states) were below 3million people. Hence, the distribution had a long right tail.
c. Population of 21 states were less than 3million, followed by 9 states each in 3.1-5.6, 5.7-8.2 million brackets. There were 4 states with population between 8.3million and 10.8 million people, and 3 states had population between 10.9million and 13.4million people. Hence, almost all the states had population below 13.4million except four outlier states with populace higher than 13.5million.
Week 4: Question 2
a. The joint probability table is in Table 7.
Table 7: Joint probability table for use of social media by gender
|
Joint Probability |
Uses Social Media and Other Websites to Voice Opinions About Television Programs |
Doesn’t Use Social Media and Other Websites to Voice Opinions About Television Programs |
Total |
|
Female |
0.290 |
0.213 |
0.503 |
|
Male |
0.237 |
0.260 |
0.497 |
|
Total |
0.526 |
0.474 |
1.00 |
b. P (Respondent is a female) = 0.503 (from the table 7) Calculation: P (Respondent is a female) = Total Females / Total Users = (395 + 291) / 1364 = 0.503.
c. P (“Respondent uses social media and other websites to voice opinions about television programs”/ Respondent is a female) = Female respondents using social media / Total females = 395 / (395 + 291)=395/ 686=0.576.
d. Event: F = the respondent is female
Event: A = the respondent uses social media to voice opinion
P (A) = 0.526 (Table 7), P (F) = 0.503 (Table 7)
P (A & F) = 0.290 (Table 7) (Cell: First row first column).
Now, P (A & F) ? P (A) * P (F)
Hence, P (A) and P (F) are not statistically independent.
Week 5: Question 3
According to the question: X = salary of a LU graduate follows normal distribution with mean = µ = $20,000 and ? = $8,000.
a. P (X > = $30,400) = P (Z > = (30,400 – 20,000)/ 8000) = P (Z > = 1.3), where Z is the Standard Normal Variate.
Using standard normal table we get, P (Z < 1.3) = 0.9032
So, P (Z > = 1.3) = 1 – 0.9032 = 0.0968.
Hence, there is approximately probability of 0.097 for a LU graduate to get at least salary of $30,400.
b. P (X = $30,400) = 0 as probability of a fixed point in a continuous distribution does not exist.
c. P (X < $15,600) = P (Z < (15,600 – 20,000)/ 8000) = P (Z < -0.55) = P (Z > 0.55) (as normal distribution is symmetric).
Now, using standard normal table we get, P (Z < 0.55) = 0.079
So, P (Z > 0.55) = 1 – 0.079 = 0.291
Hence, 29.1 percentages of students can get the tax break.
d. P (X > = $32,240) = P (Z > = (32,240 – 20,000)/ 8000) = P (Z > = 1.53), where Z is the Using standard normal table we get, P (Z < 1.53) = 0.937 So, P (Z > = 1.53) = 1 – 0.937 = 0.063.
Now, let there be N number of students graduated this year from this university.
So, N*0.063 = 189 => N = 3000
Hence, 3000 students graduated this year from this university.
Week 6: Question 3
According to the problem:
µ-CR = 502 and ?-CR = 100
µ-M = 515 and ?-M= 100
µ-W = 494 and ?-W = 100
N = 90
a. P (|x-bar - µ-CR| < 10) =P ( |Z| < 10/ (100/?90)) = P (-0.95 < Z < 0.95) = 2*P (Z < 0.95)
Using standard normal table we get, P (Z < 0.95) = 0.829
So, P (0 < Z < 1.53) = 0.329
Hence, P (|x-bar - µ| < 10) =2*P (Z < 0.95) = 2*0.329 = 0.658
Therefore, there is probability of approximately 0.66 that test takers will score within 10 points of 502.
b. P (|x-bar - µ-M| < 10) =P ( |Z| < 10/ (100/?90)) = P (-0.95 < Z < 0.95) = 2*P (Z < 0.95)
Using standard normal table we get, P (Z < 0.95) = 0.829
So, P (0 < Z < 1.53) = 0.329
Hence, P (|x-bar - µ| < 10) =2*P (Z < 0.95) = 2*0.329 = 0.658
Therefore, there is probability of approximately 0.66 that test takers will score within 10 points of 515.
Probabilities in both the parts are same since difference between sample and population means are same (difference of 10 points in each case). Also, standard deviation and sample sizes are also identical. Therefore, the probabilities are also equal.
References
Hoelter, L., Pienta, A., & Lyle, J. (2016). Data preservation, secondary analysis, and nbvcReplication: Learning from existing data. The SAGE Handbook of Survey Methodology, 651-661. https://doi.org/10.4135/9781473957893.n40
Lacort, M. O. (2014). DESCRIPTIVE STATISTICS. Statistics assignment In Descriptive and inferential statistics - Summaries of theory and exercises solved (1st ed., pp. 13-50). Lulu.com.
Siegel, A. (2016). Introduction and Descriptive Statistics. In Practical business statistics (7th ed., pp. 3-18). Academic Press.
Wuensch, K. L. (2014). Scales of measurement. Wiley StatsRef: Statistics Reference Online, 70-120. https://doi.org/10.1002/9781118445112.stat06378