Statistics Assignment: Business Report On Performance Of Australian Business School Students In Management Accounting Subject

Question

Task: Assignment report on students’ performance in Management accounting subject
An Australian Business School is keen to improve students’ performance in the subject of Management accounting, and understand important differences in students’ performance across gender, campuses, trimesters and student status.

Assume you work as an Analyst for this Business school and you have been asked to study the current students’ performance. You have collected data for 362 students taking the subject in the Business School. The data is on an excel file named “Marks Accounting”. The data collected are recorded in the file as follows:

Mark Mark of each student
Trimester 1 for trimester 1, 2 for trimester 2 and 3 for trimester 3
Status 1 for Domestic students, 2 for International students
Gender 1 for female and 2 for male
Campus 1 for Sydney campus and 2 for Wollongong campus

Assignment Tasks:
1. Visually present data for the marks from different trimesters. Calculate descriptive statistics for the marks of different trimesters. Comments on the location, shape and variability of those distributions.

2. Visually present data for the marks for domestic and international students. Calculate descriptive statistics for the marks of domestic and international students. Comments on the location, shape and variability of those distributions.
3. Visually present data for the marks of students in trimester 3 for domestic and international students. Calculate descriptive statistics for the marks of students in trimester 3 by domestic or international status. Comments on the location, shape and variability of those distributions.
4. Many academics at business school believe that female students have higher marks than male students in accounting area. How do you test whether the average mark in female students is significantly higher than the average mark of male students? Use appropriate inferential statistical techniques.
5. Using the data collected, how do you test the claim that there is no significant difference of the average marks of students from the different trimesters? What do you find from your analysis? Use appropriate inferential statistical techniques.
6. The Business School is interested in understanding the performance of domestic and international students. How do you test whether there is a significant difference of average marks across the two groups? Use appropriate inferential statistical techniques.
7. Many academics at business school believe that Wollongong students perform better than Sydney students. How do you test whether the average marks of Wollongong students is higher than the average mark of Sydney students? Use appropriate inferential statistical techniques .

More information on this assessment will be provided during the session time including the presentation of the assignment and submission to Turnitin. Please note that you should submit the assignment according to the format given in the Moodle site.

Answer

Executive Summary:
The business report intends to find whether the performance of Australian Business School students in Management accounting differs due to gender, campuses, trimesters and status of students or not. For understanding the consequences of those variables, the report takes sample of 362 students and collect data to perform statistical analysis. Based on the requirement, the report uses descriptive statistics and inferential statistical techniques. From the finding, it is obtained that the performance of students differ in different semesters but these do not depend on any categorical variable. Hence, the university needs to analyse other external and internal issues in this aspect.

Business Problem:
This business report intends to analyse students’ performancein an Australian Business School. The main focus of the report is to understand how students’ marks differ in Management accounting subjectand whether gender, campuses, trimesters and status of students influence it or not. As an analyst of the specified business school, I have collected data from students of management accounting to conduct statistical analysis. The entire business report discusses some statistical problems and its analysis to deliver a conclusion of the report and recommends more actions to develop performance of students on management accounting subject.

Statistical Problem:
The data is collected for 362 students and conduct different statistical analysis as per the requirement with the help of MS Excel software. In the collected data set, trimester, status, gender and campus represent categorical variables. To present data visually, the report measures descriptive statistics with which it interprets location, shape as well as variability of the distribution of a particular variable. Descriptive statistics provides a summary of a particular data set and represents the entire sample. For testing hypothesis, the report considers two sample t-tests with equal variance at 5% significance level. Furthermore, the report takes one-way ANOVA to measure whether the averages of two independent groups has any statistically significant difference or not. The two methods of hypothesis testing have a basic difference. T-test is applied to compare average of two samples or population while for comparing means of more than two samples or population, one uses ANOVA. The following section describes the statistical outcomes with detail discussion.

Analysis:
Task 1:
In the first task, the report focuses the marks of 362 students from different semesters. Here, semester 1 is represented as 1 while semester 2 and 3 are represented as 2 and 3 respectively. The main purpose of the report is to analyse and describe the data visually with suitable graphical presentation. Furthermore, the report aims to calculate descriptive statistics for measuring the location of the collected data along with shape and variability of data distribution for these 3 distinct groups. Location and shape for a particular data set is measured with the help of central tendency, viz. mean, median and mode. Variability of data is measured with the help of variance (Ho and Yu 2015). For a symmetrically distributed data set, the value of mean and median is same. However, in case of skewed distribution, the difference between mean value and median value can be observed. In case of positively skewed data, the mean value is always higher than median while median is always higher than mode value. On the contrary, for a negatively skewed data, the mean is always smaller than median and median is smaller than mode.

Figure 1 is the histogram that represents the data of semester 1 graphically. This graphical display reflects the spread and shape of the data set with bars having unequal height. However, the width of each bar in the histogram is same due to the same class width. From the figure, it can be seen that most of the students receive marks between 51 and 60 in management accounting during the 1st semester.

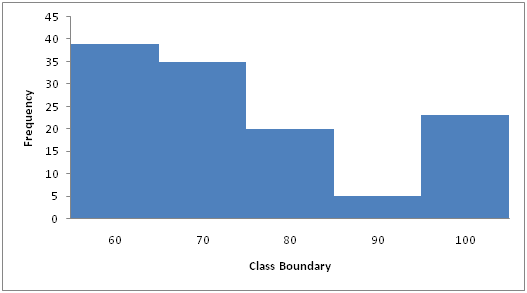
Figure 1: Histogram for Semester 1>

Table 1: Descriptive statistics for Semester 1 marks

MARK (1)

From figure 1 and table 1 it can be seen that the value of marks in semester 1 is positively skewed as the value of mean (69.82) and median (66.11) is higher than mode (59.71). Hence, the shape of the data set is measured with the help of its location. The variance of the data set is 218.46 which indicate that the random variable differs from the mean value noticeably. Moreover, the range of the data set is (98.66-50.84) = 47.82

Figure 2: Histogram for Semester 2
Figure 2 visually represents the data of semester 2 with the help of a histogram. From the figure, it can be seen that most of the students receive marks between 47 and 57 in management accounting during the 2nd semester.

Table 2: Descriptive statistics for Semester 2 marks
MARK (2)

From figure 2 and table 2 it can be seen that the value of marks in semester 2 is positively skewed as the value of mean (52.54) and median (49.19) is higher than mode (42.4). Thus, the shape of the data set is measured with the help of its location values. The variance of the data set is 93.39 which indicate that the random variable differs from the mean value but as much as semester 1. Moreover, the range of the data set is (73.3-38.63) = 34.67, which also indicates that the spread of semester 2 marks is comparatively less than that of semester 1.

Figure 3: Histogram for Semester 3
Figure 3 visually represents the data of semester 3 with the help of a histogram. From the figure, it can be observed that most of the students receive marks between 35 and 45 in management accounting during the 3rd semester.

Table 3: Descriptive statistics for Semester 3 marks
MARK (3)

From figure 3 and table 3 it can be observed that the value of marks in semester 3 is positively skewed as the value of mean (43.75) and median (44.38) is higher than mode (42.52). The variance of the data set is 61.95 which show that the random variable differs from the mean value but not significantly. Moreover, the range of the data set is (58.73-26.18) = 20.10, which also indicates that the spread of semester 3 marks is comparatively less than that of previous two semesters.

Task 2:

Figure 4: Histogram for marks of domestic students

Figure 4 visually represents the data of marks obtained by domestic students in all over semesters with the help of a histogram. According to the figure, it can be observed that most of the students receive marks from 47 to 57 in management accounting during the trimester.

Table 4: Descriptive statistics for marks of domestic students
MARK(D)

According to figure 4 and table 4, it can be observed that the value of marks in all over semesters is positively skewed but almost symmetrical.This is because the value of mean (55.05) and median (54.31) is higher than mode (52.37). The variance of the data set is 210.71 which show that the random variable differs from the mean value significantly. Moreover, the range of the data set is (98.23-27.9) = 70.33, which also indicates that the spread of marks of domestic students islarge.

Figure 5: Histogram for marks of international students

Figure 5 visually represents the data of marks obtained by international students in the overall trimesters with the help of a histogram. According to the figure, it can be observed that most of the students receive marks from 46 to 56 in management accounting during the trimester.

Table 5: Descriptive statistics for marks of international students
MARK (I)

As per figure 5 and table 5, it can be observed that the value of marks in all over semesters is positively skewed. This is because the value of mean (55.92) and median (51.07). However, the value of mode is higher than median and mean. The variance of the data set is 268.45 which show that the random variable differs from the mean value significantly. Moreover, the range of the data set is (98.66-26.18) = 72.48, which also shows that the spread of marks of international students is comparatively low.

Task 3:

Figure 6: Histogram of trimester 3 marks of domestic students

Figure 6 visually represents the data of marks obtained by domestic students in trimester 3 with the help of a histogram. As per the figure, that maximum number of the students receives marks between37 and 47 in management accounting during.

Table 6: Descriptive statistics for Semester 3 marks of domestic students
MARK(D)

As per figure 6 and table 6, it can be observed that the value of marks in all over semesters is positively skewed but almost symmetric. This is because the value of mean (44.85) and median (44.18) are almost the same. However, the value of mode is lower than median and mean. The variance of the specified data is 65.95 which show that the random variable differs from the mean value not significantly. Moreover, the range of the data set is (58.73-27.9) = 30.83, which indicates that the spread of marks in case of international students is comparatively low.

Figure 7: Histogram oftrimester 3 marks of international students

Figure 7 visually represents the data of marks obtained by international students in trimester 3 with the help of a histogram. As per the figure, that maximum number of the students receives marks between 36 and 46 in management accounting during.

Table 7: Descriptive statistics for Semester 3 marks of international students
MARK (I)

As per figure 7 and table 7, it can be observed that the value of marks in all over semesters is negatively skewed. This is because the value of mean (42.33) is less than median (45.53). However, the value of mode is lower than median. The variance of the data set is 54.33 which show that the random variable differs from the mean value slightly. Moreover, the range of the data set is (52.15-26.18) = 25.97, which indicates that the spread of marks of international students is small

Task 4:
The report tries to analyse whether the female students get higher marks in management accounting compared to male students or not (Amrhein, Trafimow and Greenland 2019). Let, the null hypothesis is:
Null hypothesis (H0): the female students do not get higher marks in accounting area than male students.

The alternative hypothesis is:
Alternative hypothesis (H1): the female students get higher marks in accounting area than male students. For testing the hypothesis, the report considers two-sample t-test with equal variance as the number of variables is two.

Table 8: t-Test: Two-Sample Assuming Equal Variances

From table 8, it can be observed the number of female students is 162 in the sample while the number of male students is 200. Hence, the average value of marks of female students is 61.83 in entire semesters while that of male students is 50.41. Furthermore, the value of variance indicates that the number between two female students differs significantly but for male students marks vary by 65.41 from the average one. At 5% significant level the value two-tail P is 0. The value is less than 0.05. Therefore, in this situation, the report rejects null hypothesis and accepts the alternative one. Therefore, the ultimate outcome is the female students get higher marks in accounting area than male students.

Task 5:
The report conducts one-way ANOVA to understand whether average marks of students from 3 semesters have significant difference or not. As the number of variables is three, the test is conducted with the help of ANOVA with one factor. For testing hypothesis, the report considers null hypothesis as well as alternative hypothesis.
The null hypothesis (H0): No major difference can be observed for the average marks of both domestic as well as international students from the 3 semesters
The alternative hypothesis (H1): There is major difference of the average marks for domestic as well as international students from the 3 semesters

Table 9: One-way ANOVA

Here, the p value is 0.00 at 5% significant level which implies that the p-value is less than 0.05. Hence, the null hypothesis is rejected and alternative hypothesis is accepted. Therefore, it is observed that there is a major difference between the average marks of domestic and international students over the 3 semesters.

Task 6:
The report intends to identify whether the average marks of domestic students and that of international students has any major difference or not. Let, the null hypothesis is:
Null hypothesis (H0): The average marks between domestic and international students does not have any significant difference The alternative hypothesis is:
Alternative hypothesis (H1): The average marks between domestic and international students have major difference For testing the hypothesis, the report selects two-sample t-test with equal variance:

Table 10: t-Test: Two-Sample Assuming Equal Variances

From table 10, it can be observeddomestic students are 165 in the sample while international students are 197. Hence, the average value of marks of domestic students is 55.05 in the trimester while that of international students is also 55.92. Furthermore, the value of variance indicates that the marks of domestic students vary from its mean value significantly but not like international students. At 5% significant level the value two-tail P is 0.6 which is higher than 0.05 (Cox 2018). Hence, in this situation, the report accepts null hypothesis and rejects the alternative one. Therefore, it can be stated that the average mark between domestic as well as international students has significant difference.

Task 7:
The report further tries to analyse whether the average marks of Wollongong students is better than that of Sydney students or not. Hence, from the analysis the report will understand the performance of students from these two locations to compare their performance. Let, the null hypothesis is:
Null hypothesis (H0): The average mark between Wollongong and Sydney students does not have any significant difference The alternative hypothesis is:
Alternative hypothesis (H1): The average mark between students of Wollongong and Sydney has any significant difference For testing the hypothesis, the report selects two-sample t-test with equal variance:

Table 11: t-Test: Two-Sample Assuming Equal Variances

From table 11, it can be observed the number of Sydney students is 201 in the sample while the number of students in Wollongong is 161. Hence, the average value of marks of Sydney students is 48.70 in the overall trimesters while that of Wollongong students is also 64.04. Furthermore, the value of variance indicates that the marks of Sydney students vary from its mean value significantly though the variation of marks of Wollongong students from the mean value is comparatively higher than that. At 5% significant level the value two-tail P is 0.0 which is less than 0.05. Hence, in this situation, the report considers the null by rejecting the alternative one. Thus, it can be stated that the average mark between Wollongong and Sydney students does not have any significant difference or in other words, the performance of Sydney students and Wollongong students is same.

Conclusion:
From the entire statistical analysis, the business report tries to come to the conclusion that whether students’ performance depend on gender, campuses, trimesters or status or not. To understand the impact of these independent variables on the marks obtained by the students in accounting area, the report applies descriptive statistics and inferential statistics techniques. It is observed that the students get highest marks on an average during 1st semester compared to semester 2 and 3. The positively skewed curve implies that the mean is higher than the median. Furthermore, the report also finds that the average highest marks of students of domestic and international are almost same and for during the total semesters. Hence, it can be stated that the marks of domestic and international studentsdo not differ significantly over the semesters. It is also observed that the female students get higher marks in management accounting compared male students. The report also observes that the average marks of students from the different trimesters have significant difference. This implies that both students of international and domestic get different scores in different semesters. Moreover, the report also observes that the performance of students do not depend on location. Hence, it can be concluded that the marks of students varies semester wise as per the syllabus.

Implications:
Therefore, from the above findings, it can be stated that the marks and performance of students do not depend on any categorical variables. Instead it depends on the study and learning capacity of students. Therefore, the university needs to find and analyse other external and internal factors that can influence the performance of students in order to help them to get higher marks in the subject.

References:
Amrhein, V., Trafimow, D. and Greenland, S., 2019. Inferential statistics as descriptive statistics: There is no replication crisis if we don’t expect replication. The American Statistician, 73(sup1), pp.262-270.
Cox, D.R., 2018. Applied statistics-principles and examples. Routledge.
Ho, A.D. and Yu, C.C., 2015. Descriptive statistics for modern test score distributions: Skewness, kurtosis, discreteness, and ceiling effects. Educational and Psychological Measurement, 75(3), pp.365-388.